Informing better decisions in global health
We use cutting-edge methods and tools to turn data into knowledge that saves lives.
Approach
Case Study
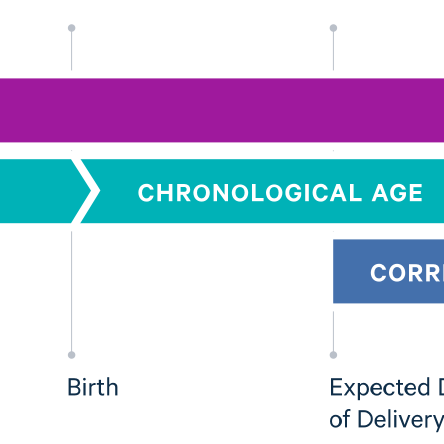
Evaluating the Feasibility of Using Algorithms to Stratify Pregnancy Risk
In just three or four months, we’ve made what would have been three or four years of progress during normal times.
Read MoreKi can help solve global challenges in global health.
Learn how researchers have used Ki's approach to break new ground.
Our WorkOur Mission
Every clinician and health policymaker has the knowledge they need to make the best decisions possible to improve people’s lives.
MissionKi uses state of the art methods and tools.
We've shared our models and tools so that you can use them in your work. Browse our resources:
Resources